Мы пока что не рассматриваем конкретную дедуктивную систему, а лишь говорим об общих свойствах всех дедуктивных систем. Уже с помощью этих весьма общих и простых знаний, можно обнаружить логические слабости и ошибки, развеять давние предрассудки, связанные с логикой. Один такой предрассудок мы уже рассмотрели, показав, зачем нужны аксиомы, и в чем состоит их практический смысл.

На графических схемах вывода наглядно видны слабости в логических рассуждениях. Рассмотрим, к примеру, вот такую схему рассуждения:

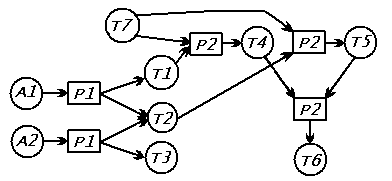
Чем она отличается от предыдущей схемы? Тем, что вместо аксиомы A3 использована теорема T7. Даже если правило вывода P2 допускает вывод из T7, сама теорема T7 не выведена ниоткуда. Этот пример иллюстририует самое простое нарушение логики: применение в доказательстве ранее недоказанных утверждений без вынесения их в аксиомы. Фактически T7 является скрытой, спрятанной аксиомой. Но аксиома не должна быть спрятана! Иначе, когда возникнет вопрос о применении теории, будут проверены аксиомы A1 и A2 и будет сделано заключение, что теорию применять можно. И будет применена теорема T6. Но мы не проверили скрытую аксиому T7! Если окажется, что она в данном случае тоже работает, все в порядке. Но если окажется, что T7 не работает, то и теорема T6, возможно, не будет работать.

Таким образом, мы приходим к правилу: всякое недоказанное утверждение должно быть или доказано, или явно причислено к аксиомам. Это правило иногда называется законом достаточного основания. В противном случае теория, построенная на дедукции, автоматически теряет главное свое свойство, которое ей придают аксиомы. Теперь перед применением любой теоремы этой теории будет уже недостаточно проверить только несколько аксиом. Вместо этого придется запоминать для каждой теоремы, какие дополнительные проверки надо выполнить, чтобы ее применить. И вместо однократной проверки, придется проверять постоянно, на каждом шагу. Конечно, это очень неудобно. Это повышает и шанс ошибиться, и шанс быть обманутым.

Предположим, мы хотим намеренно обмануть собеседника и скрыть тот факт, что теорема T7 не доказана. В нашей схеме тот факт, что она не доказана, слишком заметен. Ни одна стрелка не ведет к T7. Как можно скрыть этот факт? Одно из распространенных ухищрений состоит в том, чтобы ввести несколько утверждений-теорем и соединить их в кольцо, где одно из звеньев в цепи доказательств не было доказано. Заметьте, что замыкание цепи шагов доказательства в кольцо - это еще не ошибка. Ошибка в том, что мы вставляем в эту цепь недоказанное утверждение и пытаемся свои действия замаскировать. Этот прием в обиходе называют "порочным кругом". Рассмотрим пример:

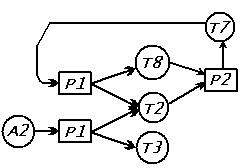
Казалось бы, выглядит все хорошо. В каждую теорему ведут стрелки и это, вроде бы, означает, что все они доказаны. Ан нет. Теорема T7 не может быть доказана до тех пор, пока не будет доказана T8, а T8 не может быть доказана до тех пор, пока не будет доказана T7. В каком порядке мы бы ни пытались доказать эту схему, мы сможем доказать T2 и T3, но T8 и T7 - не сможем. В какой-то момент нам приется сослаться на еще не доказанную теорему.

Например так: "Из A2 по правилу P1 получим T2 и T3. Из T3 (которую мы только что доказали) и T8, (которую мы докажем чуть позже) по правилу P2 получим T7. Из T7 (которую мы только что доказали) получим T2 (которую уже однажды доказали ранее) и T8 (которую обещали доказать позднее, и сдержали это обещание).

Хитрость заключается в том, что мы "пообещали" доказать в будущем то, что еще не доказали. Да, обещание мы свое сдержали, но основной принцип дедуктивного метода нарушили. Подобное жульничество легко распознается, если потребовать: всякое доказательство должно быть последовательным, нельзя доказывать теоремы на основе теорем, которые еще не доказаны. Если расписать ход доказательства, то получим:

A2 T2, T3 // P1
T2, T8 T7 // P2 - ошибка в доказательстве подчеркнута
T7 T2, T8 // P1

Таким образом, если ваш собеседник пытается использовать некоторое утверждение X, которое обещает доказать "позднее", это, вполне возможно, говорит о попытке вас обмануть. Даже если он действительно приведет доказательство X позднее, может оказаться, что в этом самом доказательстве он использовал факт Y, который раньше доказал на основе X. Образуется порочный круг, маскирующий логическую ошибку. Разумеется, может быть и так, что ничего такого не случится, X будет честно доказано, но зачем рисковать? Если известен простой и надежный способ избегать ошибок, то надо ему следовать. Таким образом, возмите за правило и требуйте от других, чтобы любое утверждение доказывалось или заранее, или непосредственно перед первым применением. Всякое обещание доказать потом, или ссылки на то, что доказательство находится в следующей главе или более поздней части книги должны вас насторожить. "На потом" можно отложить многие вопросы - но не доказательства.

Заметим, что само по себе наличие циклов в доказательстве еще не является нарушением логики. Рассмотрим следующий пример:

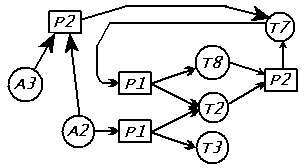
Здесь имеется тот же самый цикл. Однако доказательство правильно, поскольку для всех теорем есть цепочки рассуждений, идущие от аксиом, например, для теоремы T7 появилась цепочка, ведущая от аксиом A2 и A3. Проблема не в цикличности, а в том, что цикличность часто используется для маскировки нарушения главного правила: ничто не должно быть доказано на основе еще не доказанного. Логические рассуждения можно замыкать в круги, но движение по такому кругу должно начинаться с доказаных ранее суждений. В данном случае можно сколь угодно долго ходить по кругу, если "войти в круг" по правильному пути, ведущему от аксиом:

A2, A3 T7 // P2
T7 T2, T8 // P1
T2, T8 T7 // P2 - ошибки нет
T7 T2, T8 // P1
T2, T8 T7 // P2

- здесь мы трижды прошли через T7, но мы не сделали ни одного "запретного" шага от недоказанного к доказанному.

И еще один вид логической ловушки. Он связан с тем, что мы привыкли помнить: аксиомы - не доказываются в рамках теории. Но забываем: правила вывода тоже не доказываются в рамках теории (!). С этим связаны две опасности. Во-первых, можно незаметно применить новое правило вывода и ваш скептицизм не забьет тревогу. Во-вторых, перед применением общепринятой теории можно проверить все аксиомы, но забыть проверить правила вывода. Второе обычно не так опасно, поскольку правила вывода в серьезных теориях часто оказываются еще надежнее, чем аксиомы. Но все же, бывает, возникают и такие случаи.

Гораздо чаще мы сталкиваемся с первой ситуацией: незаметно и скрытно наш собеседник применяет новое правило вывода. Обычно оно извлекается из другой теории, в которой работает более-менее успешно, но в данной теории уже не работает. Или берется из очень ненадежной, слабой теории. Очень характерна, к примеру, такая ситуация, когда философ в споре с физиком употребляет чисто философское правило вывода, например "все должно иметь причину". При этом продолжает требовать точности результатов на уровне физики, а не на уровне философии.