Практические советы и замечания

[предыдущая глава]  [оглавление]  [следующая глава]

Как выполнить преобразование на практике

Берем сигнал длительностью T, разбиваем его на N - 1 частей, получаем мгновенные значения сигнала в N точках:

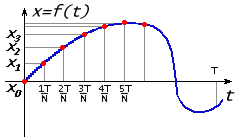
Если есть возможность выбрать N, то следует выбрать степень двойки, так как соответствующий алгоритм немного быстрее. Если нет возможности выбрать, то не страшно - все равно есть алгоритм, не такой быстрый, но тоже имеющий сложность N log₂N.

Далее, создаем массив комплексных чисел, длиной N:

    ShortComplex arr[N];

Теперь заполняем его. Допустим исходный сигнал у нас в массиве x, и это действительная величина. Тогда просто копируем x в реальную часть элементов в массиве arr, а мнимую часть обнуляем:

    for(int i= 0; i < N; ++i)
    {
        arr[i].re= x[i];
        arr[i].im= 0.0;
    }

Теперь осталось применить алгоритм БПФ. Если N = 2^k - т.е. степень двойки, то используем соответствующий алгоритм отсюда:

    fft(arr, k, false);

Если же мы не можем гарантировать, что N - степень двойки, тогда используем универсальный алгоритм отсюда:

    universal_fft(arr, N, false);

После исполнения этой функции массив arr изменится и будет теперь содержать результат прямого преобразования Фурье.

Для обратного преобразования надо вызвать ту же функцию с последним аргументом true. Если нужна действительная функция x, то надо будет еще скопировать массив обратно, отбрасывая мнимую часть:

    universal_fft(arr, N, true);

    for(int i= 0; i < N; ++i)
        x[i]= arr[i].re;

Наглядное представление

Полученный результат представляет собой последовательность комплексных чисел в форме пар: (реальная часть, мнимая часть). Но для понимания физической структуры сигнала желательно преобразовать их в амплитуды, частоты и фазы гармоник.

Для преобразования можно использовать формулы:

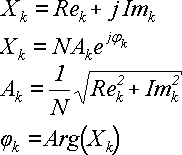
Самый первый элемент с индексом 0 показывает постоянную составляющую сигнала, то есть, насколько он в среднем "приподнят" над осью времени. Остальные элементы представляют гармоники вида A cos(2πνt + φ), где ν - это частота, которая для гармоники с индексом k будет равна:

ν = k / T

Часто бывает дано не суммарное время сигнала T, а частота дискретизации: сколько отсчетов приходится на одну секунду. Обозначим ее S. Тогда частота для гармоники с индексом k будет равна:

ν = S k / N

В сумме постоянная составляющая и все гармоники должны дать исходный сигнал.

Также по ходу дела можно исправить зеркальный эффект. Если взять сигнал, который состоит из единственной гармоники с частотой f > 0 и выполнить прямое дискретное преобразования Фурье, то в полученном спектре обнаружатся два ненулевых элемента, соответствующих частотам f и f' = (N / T - f), где N - число точек дискретного преобразования Фурье, T - длительность отрезка, для которого выполнено преобразование. Оба элемента имеют половинные амплитуды по сравнению с исходной гармоникой.

Для устранения зеркального эффекта можно просто обнулить вторую половину спектра с индексами после N / 2, а все элементы первой половины помножить на 2. При этом не надо умножать самый первый элемент с индексом 0, который соответствует частоте 0, то есть постоянной составляющей.

В процессе преобразования могут возникнуть ошибки округления, из-за которых появятся ненулевые элементы там, где должен быть ноль. Если мы хотим устранить этот эффект, нужно задать некоторый нижний предел и отбрасывать гармоники с амплитудами меньше этого предела.

И, наконец, последний штрих: функция синуса которая начинается от нуля, может оказаться нагляднее, чем функция косинуса. Поэтому есть смысл представить гармоники в виде синусов: A sin(2πνt + φ), только для этого придется сместить фазу на π/2.

В результате алгоритм получения наглядного представления будет таким:

    //Это комплексные числа, результат прямого дискретного преобразования Фурье
    //ShortComplex - это структура с полями: double re, im;
    ShortComplex arr[N];
	
    //это индекс комплексного числа в массиве arr
    int i;

    //это частота дискретизации
    double nSamplesPerSec;

    //убираем зеркальный эффект, просто отбрасывая вторую половину
    int Nmax= (N + 1) / 2; 

    //мы хотим получить массив гармоник.
    //это массив амплитуд, массив частот и массив фаз для каждой гармоники
    double *freq= new double[Nmax];
    double *amp= new double[Nmax];
    double *phase= new double[Nmax];
	
    //это индекс гармоники. в конце алгоритма он будет равен количеству найденных гармоник
    int j= 0;

    //это нижний предел амплитуды гармоники. тут может быть число больше нуля
    //в зависимости от того, какие амплитуды мы считаем ничтожно малыми.
    double limit= 0.001;
    
    //вспомогательная переменная для оптимизации
    double abs2min= limit * limit * N * N;
	
    //получаем постоянную составляющую
    if (arr[i]->re >= limit)
    {
        amp[j]= arr[i].re / N;
		freq[j]= 0.0;
		phase[j]= 0.0;
		++j;
    }
    ++i;

    //получаем остальные гармоники
    for(i= 1; i < Nmax; ++i)
    {
        double re= arr[i].re;
        double im= arr[i].im;
		
        //это квадрат модуля комплексного числа arr[i]
        double abs2= re * re + im * im;
		
        //отбрасываем слишком слабые гармоники
        if (abs2 < abs2min)
            continue;
		
        //вычисляем апмлитуду. 2.0 - для устранения зеркального эффекта
        amp[j]= 2.0 * sqrt(abs2) / N;
		
		//вычисляем фазу косинуса в радианах
        phase[j]= atan2(im, re);

        //преобразуем косинус в синус. M_PI2 = пи/2, M_PI = пи
		//в результате фаза будет в диапазоне от -пи/2 до +пи/2
        phase[j]+= M_PI2;
        if (phase[j] > M_PI)
            phase[j]-= M_2PI;
		
        //можно еще преобразовать радианы в градусы
        phase[j]= phase[j] * 180.0 / M_PI;
		
		//получаем частоту
        freq[j]= (nSamplesPerSec * i) / N;
		
        ++j;
    }
	

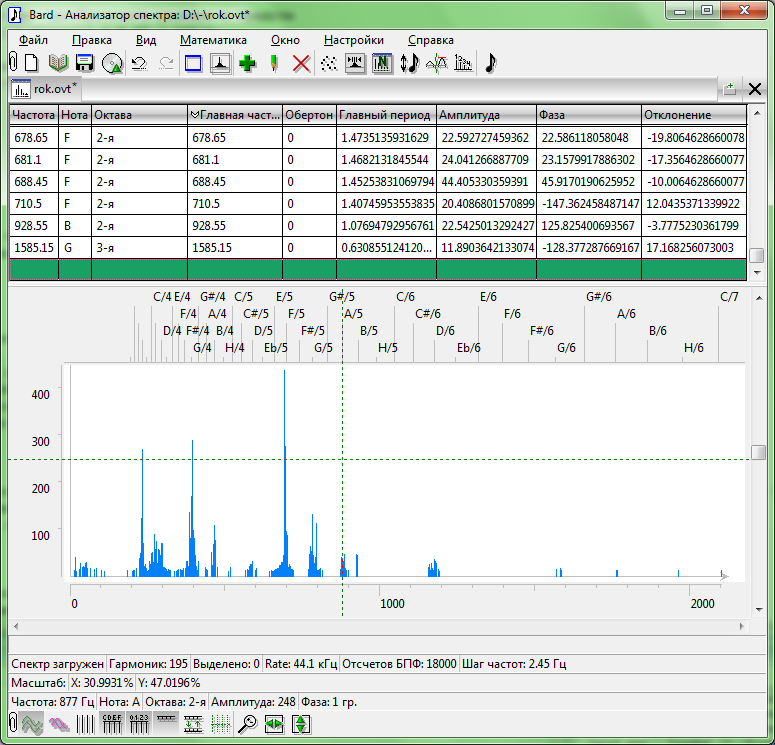
Получив список частот, фаз и амплитуд, можно воспользоваться какой-нибудь программой, чтобы построить график или таблицу. Например, в очередной версии программы Bard, которую я сейчас пишу, это выглядит так:

Преобразование туда и обратно

Если выполнить прямое, а потом обратное преобразование Фурье, то должны получиться те же самые числа с небольшими отклонениями из-за неизбежных ошибок округления. В частности, если исходная последовательность была действительной (мнимые части равны нулю), то после прямого преобразования Фурье могут появиться ненулевые мнимые части, но после обратного преобразования они снова обнулятся.

Однако, если после прямого преобразования внести изменения в массив и потом выполнить обратное преобразование, то могут появиться элементы с ненулевыми мнимыми частями. Если вы применяете преобразования Фурье для обработки действительных сигналов, эти ненулевые мнимые части надо просто игнорировать.

В частности, если вы исправляете зеркальный эффект, вы (после прямого преобразование) обнуляете элементы с индексами выше N / 2 и удваиваете элементы с индексами от 1 до N / 2. Если теперь выполнить обратное преобразование, то реальная часть сигнала останется прежней, но мнимая часть сигнала станет ненулевой. Ее можно проигнорировать.

Эффект размазывания

Данный эффект подробно расматривался ранее, а здесь приведен среди других эффектов. Если частота исходной гармоники не равна в точности дной из частот k/T, то вместо одной линии спектра получится смазанный пик - тем более смазанный, чем дальше отстоит исходная частота от ближайшей частоты k/T.

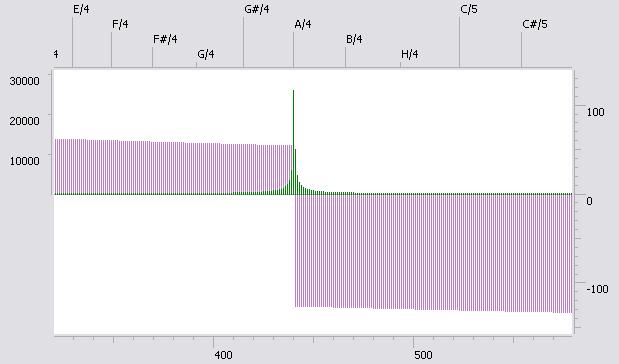
Здесь зеленым показана амплитуда спектральных гармоник, фиолетовым - фаза (как видите, в районе нужной частоты она делает резкий скачок). Исходной гармоникой здесь было колебание с амплитудой 30000, фазой 0 и частотой 440,2 Гц. Время дискретизации T было равно 1 секунде при разбиении на 44100 отрезков. Ближайшие частоты вида k/T равны 440 и 441 Гц, для них никакого размазывания не было бы.

В англоязычной литературе этот эффект называется smearing (размазывание) или leakage (рассеяние). Это связано с тем, что мощность исходной гармоники как бы рассеивается. Если вы посмотрите на предыдущую иллюстрацию, то увидите, что высота пика не дотягивает до правильной отметки в 30000, но вместе с дополнительными линиями, окружающими пик, мощность получается такой, как нужно.

Эффекты модуляции

А вот эта картинка -

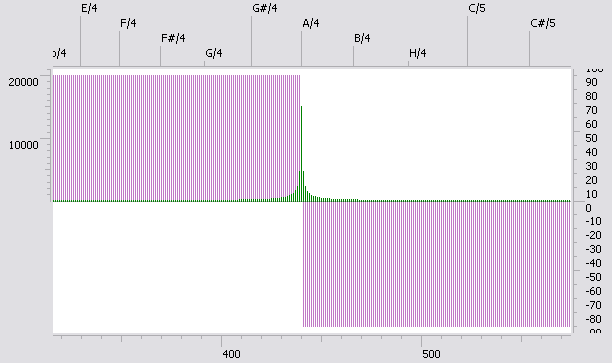
- получена совсем другим способом. Здесь была гармоника 440 Гц, но ее амплитуда в течение секунды линейно затухала от 30000 до 0. Картинки очень похожи, так что пойди разбери - то ли причина размазывания в том, что гармоника не попала точно в величину k/T, то ли в том, что было затухание во времени.

Различие там есть, просто оно не видно на картинке. При непопадании на k/T фаза максимальной гармоники приблизительно совпадает с фазой одной из двух соседник гармоник и сильно отличается от фазы другой. А при модуляции фазы соседних гармоник или совпадают, или обе сильно отличаются от фазы максимальной. Чтобы показать это, на следующей паре картинок фаза и амплитуда отмечены не вертикальными рисками, а крестиками:

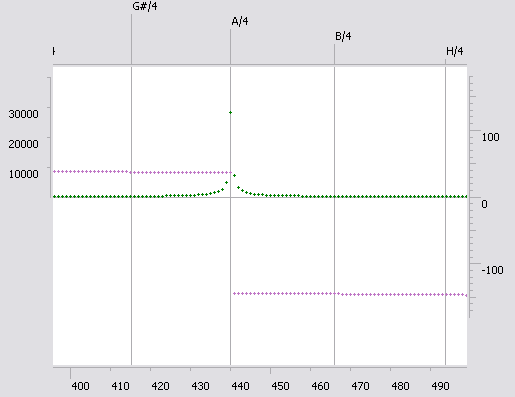
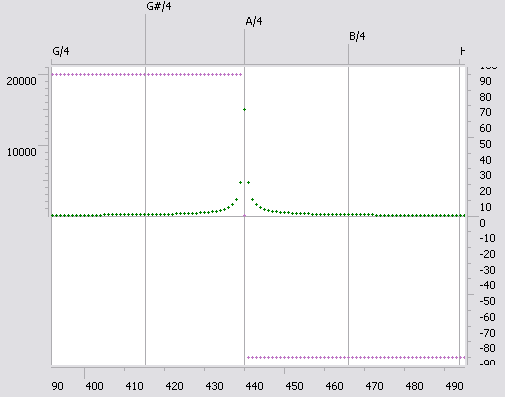
На левой картинке - размазывание от несовпадения частот, на правой - от затухания. Так что в целом для различения этих случаев можно применять критерий: если фаза максимальной гармоники где-то посредине между фазами соседних гармоник, то это - модуляция, а если фаза максимальной гармоники гораздо близка к одной из "соседок", то это - несовпадение частот.

Вот еще картинка:

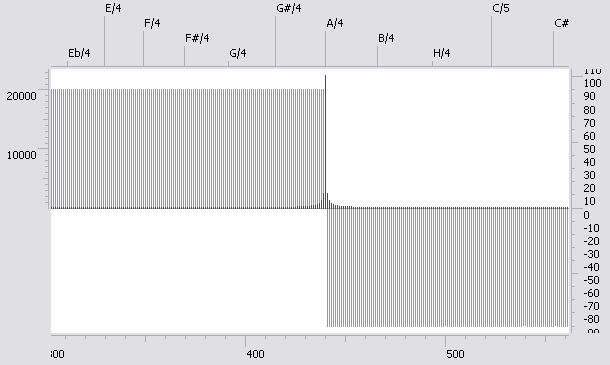
- здесь амплитуда линейно затухала от 30000 до 15000.

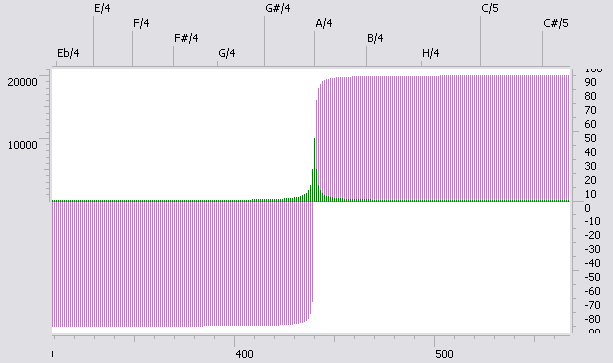
- здесь амплитуда нелинейно нарастала от 0 до 30000.

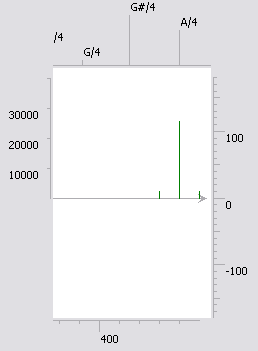
- эта скромная картинка получена с добавлением пульсации: амплитуда синусоидально увеличивается-уменьшается 10 раз за секунду. Две дополнительные частоты по бокам от основной обеспечили пульсацию основной частоты.

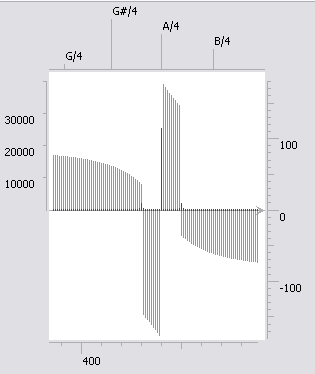
- а здесь все то же самое, но пульсация не 10 раз в секунду, а чуть-чуть медленнее. В секунду не уложилось целое число пульсаций, так что возник эффект размазывания вокруг дополнительных частот.

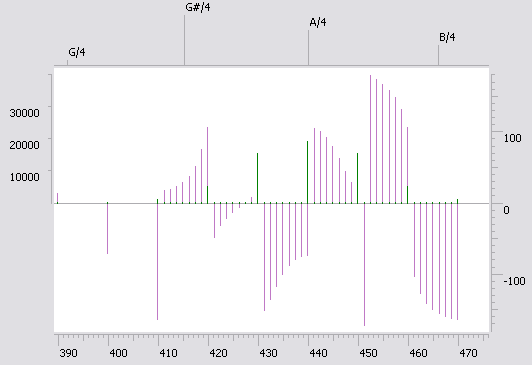
- наконец, вот этот хаос возникает в результате "вибрато" - то есть, периодического изменения не амплитуды, а частоты. В данном случае на периоде 0.8 секунд произошло 8 периодических изменений частоты на четверть тона.