Упорядоченная пара (также "кортеж") из двух аргументов (также "параметров"): x и y -
это множество {{x}, {x, y}}, сокращенно обозначаемое как (_x, y_).
Мы не используем более распространенное обозначение с угловыми скобками <x, y>,
из-за того, что их неудобно набирать в формате HTML, и из-за того, что их можно перепутать
со знаками операций "меньше"/"больше".
x и y будем называть "аргументами" или "параметрами", но не "элементами"
кортежа. Слово "элемент" уже зарезервировано для элементов множества, которые есть
{x} и {x, y}, а вовсе не x и y.
По аналогии упорядоченной тройкой (_x, y, z_) будем называть упорядоченную пару,
из двух элементов: упорядоченной пары (_x, y_) и элемента z. То есть:
(_x, y, z_) = (_(_x, y_), z_)
По индукции можно дать определение для упорядоченного набора из n элементов:
Упорядоченный набор (также "кортеж") из n элементов: x1,...xn
- это множество (_(_x1,...xn−1_), xn_),
кратко обозначаемое, как (_x1,...xn_).
Упорядоченным набором из одного элемента будем считать сам этот элемент, то есть: (_x_) = x.
Декартово произведение (также "прямое произведение") непустых множеств X и Y - это множество всех
упорядоченных пар вида (_x, y_), где x 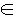 X & y
X & y 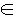 Y,
коротко обозначаемое, как X
Y,
коротко обозначаемое, как X Y.
Y.
Если X или Y - пустое, то полагается X Y =
Y = 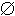 .
Декартово произведение считается бинарной операцией, дающей в результате множество, поэтому можно составить серию произведений:
X1
.
Декартово произведение считается бинарной операцией, дающей в результате множество, поэтому можно составить серию произведений:
X1 X2
X2 ...
... Xn
(порядок операций, как обычно, слева направо).
Элементами такой серии будут все возможные упорядоченные наборы вида
(_x1,...xn_) такие, что
x1
Xn
(порядок операций, как обычно, слева направо).
Элементами такой серии будут все возможные упорядоченные наборы вида
(_x1,...xn_) такие, что
x1 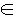 X1 & ... & xn
X1 & ... & xn 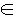 Xn
В отличии от алгебраического произведения, декартово произведение не коммутативно и не ассоциативно. То есть, перестановка
операндов и изменение порядка выполнения операций в серии могут изменить результат.
Xn
В отличии от алгебраического произведения, декартово произведение не коммутативно и не ассоциативно. То есть, перестановка
операндов и изменение порядка выполнения операций в серии могут изменить результат.
Функция - это такое непустое подмножество F некоторого множества
X Y, что для всякого элемента x из X,
найдется ровно один элемент y из Y такой, что
(_x, y_)
Y, что для всякого элемента x из X,
найдется ровно один элемент y из Y такой, что
(_x, y_) 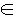 F.
F.
Здесь X есть множество определения функции F, и Y
есть множество значений функции F. Таким образом, функция также является множеством,
и можно говорить о равенстве (или одинаковости) функций, подразумевая равенство множеств.
Одновременно функция является отображением в том смысле, что всякий элемент x
из X отображается на единственный элемент y из Y такой, что
(_x, y_) 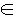 F.
F.
Важный частный случай - когда область определения сама является декартовым произведением:
X = X1 X2
X2 ...
... Xn (1)
Xn (1)
Для функций можно говорить о том, что они зависят от одной или нескольких переменных. Будем говорить,
что функция F зависит от переменных x1,...xn,
если ее область определения X есть декартово произведение из n сомножителей
как в формуле (1). Причем, мы предпочинаем обозначать аргументы элементов X
через эти переменные и в этом порядке: (_x1,...xn_) 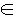 X.
Переменные x1,...xn будем называть аргументами (или параметрами)
функции F.
X.
Переменные x1,...xn будем называть аргументами (или параметрами)
функции F.
Обозначение y = F(x1,...xn)
означает, что (_(_x1,...xn_), y_) 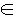 F.
Другими словами, эта формула означает, что элемент (_x1,...xn_)
из области определения отображается на элемент y из области значений. В частном
случае n = 1 формула y = F(x) означает, что (_x, y_)
F.
Другими словами, эта формула означает, что элемент (_x1,...xn_)
из области определения отображается на элемент y из области значений. В частном
случае n = 1 формула y = F(x) означает, что (_x, y_) 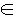 F.
Процедуру поиска подходящего y по заданным x1,...xn
будем называть вычислением значений функции F, а y - результатом
вычисления формулы F(x1,...xn).
F.
Процедуру поиска подходящего y по заданным x1,...xn
будем называть вычислением значений функции F, а y - результатом
вычисления формулы F(x1,...xn).
Вообще говоря, каждую функцию от n переменных можно рассматривать и как функцию от одной переменной,
и как функцию от любого промежуточного числа переменных. Только области значений этих переменных будут другими.
Например, функция от 3 целых переменных x, y, z отображает кортежи вида
(_x, y, z_) на область значений. Но каждый такой кортеж из трех аргументов является короткой записью
кортежа из двух элементов: (_x, y, z_) = (_(_x, y_), z_). То есть, мы можем рассматривать
его как кортеж из двух элементов (_t, z_), где z - целое, а t
- кортеж из двух целых. Так что и функцию можем рассматривать как функцию от двух переменных t
и z, причем для z область определения - множество Z всех целых чисел,
а для t область определения - множество всех упорядоченных пар из целых чисел Z Z.
Далее мы можем рассматривать каждый кортеж (_(_x, y_), z_) и вовсе как единый элемент,
обозначаемый переменной v. Получится функция от одной переменной v
с областью определения Z
Z.
Далее мы можем рассматривать каждый кортеж (_(_x, y_), z_) и вовсе как единый элемент,
обозначаемый переменной v. Получится функция от одной переменной v
с областью определения Z Z
Z Z.
Во всех трех случаях мы получим одну и ту же функцию (одно и то же множество).
Z.
Во всех трех случаях мы получим одну и ту же функцию (одно и то же множество).
Из рассмотренного примера видно, что выбор количества переменных для функции не всегда однозначен
и предусматривает несколько вариантов. Если это так, то можно выбирать тот вариант, который удобнее.
Таким образом, функция каждый раз берется одна и та же, но формат записи немного отличается.
В одних случаях может показаться более простым вместо одной переменной, обозначающей относительно
сложные объекты (упорядоченные тройки целых чисел) использовать три переменные, обозначающие
более простые объекты (целые числа). Однако важно то, что всякую функцию от некоторого количества
переменных можно рассматривать и как функцию от одной переменной. Это может быть удобно в других
случаях.
Таким образом, когда мы говорим, что "функция зависит от n переменных", то
имеется в виду, что эта функция может быть представлена в форме с зависимостью от n
переменных, но ни в коем случае не имеется в виду, что та же самая функция не может зависеть от
другого количества переменных, если будет представлена в другой форме.
Множество Xi будем называть областью определения переменной xi.
Условимся, что в пределах одного рассуждения для одинаковых (по написанию) переменных мы всегда будем выбирать одинаковые
области определения, даже если речь идет о разных функциях.
Предикат - это функция с областью значений TF.
Предикат, зависящий от n переменных, называется n-арным.
Если переменная F обозначает функцию или предикат от n переменных,
то формула F(γ1,...γn),
где γi для i = 1,..n - некоторые формулы,
обозначает тот элемент области значений функции F, на который отображается
кортеж (_γ'1,...γ'n_),
где &gamma'i - результат вычисления формулы γi.
Если все переменные имеют область определения TF, то количество различных
предикатов определенной арности ограничено. Например, тогда предикатов арности 1
всего 4 штуки. Это множества:
- {(_false, false_), (_true, false_)}
- {(_false, false_), (_true, true_)}
- {(_false, true_), (_true, false_)}
- {(_false, true_), (_true, true_)}
Предикатов арности 2 будет 16 штук, вот один из них:
{(_(_false, false_), false_), (_(_false, true_), false_), (_(_true, false_), false_), (_(_true, true_), true_)}
Другой способ задания предиката - через формулы. Будем считать, что всякая формула Ψ
булевой алгебры, содержащая n различных свободных вхождений переменных (n ≥ 0) может использоваться для
обозначения n-арного предиката. "Может использоваться для обозначения" в том смысле,
что этот предикат может быть однозначно восстановлен по формуле, если действовать согласно
описанной ниже процедуре. В дальшейшем можно будет расширить список формул, задающих предикаты.
Замечание: в формулах булевой алгебры (как мы их определили к данному моменту) все вхождения переменных
являются свободными.
Надо выписать все переменные, которые есть в формуле, в том порядке, в каком они встретились
в формуле. Если переменная встречается в формуле не в первый раз, она не учитывается.
Т.е. выписываем только первые вхождения слева направо. Получаем список переменных,
скажем: x, y, z.
Теперь определяем предикат. Он будет зависеть от n переменных, указанных в
списке. Его областью определения будет декартово произведение областей допустимых значений
для переменных, причем порядок умножения соответствует порядку переменных в списке.
Каждый кортеж из области определения будет отображаться предикатом на результат
вычисления формулы после подстановки аргументов кортежа на место соответствующих
свободных переменных в формуле.
Будем говорить в таких случаях, что предикат построен по формуле Ψ
или что формула Ψ задает (или образует) предикат.
Например, формула x & y может использоваться для обозначения предиката
арности 2, который был записан выше в канонической форме.
Переменные, выписанные в нужном порядке: x, y.
Область определения предиката есть декартово произведение TF TF,
оно включает в себя четыре кортежа:
(_false, false_),
(_false, true_),
(_true, false_),
(_true, true_). Если взять, например, кортеж (_false, true_), и
подставить в формулу, то получим false & true. Вычисление этой формулы дает
false. Теперь составим из кортежа и результата вычисления новый кортеж:
(_(_false, true_), false_). Он и будет очередным элементом предиката,
а всего таких элементов 4 - столько же, сколько элементов в области определения.
TF,
оно включает в себя четыре кортежа:
(_false, false_),
(_false, true_),
(_true, false_),
(_true, true_). Если взять, например, кортеж (_false, true_), и
подставить в формулу, то получим false & true. Вычисление этой формулы дает
false. Теперь составим из кортежа и результата вычисления новый кортеж:
(_(_false, true_), false_). Он и будет очередным элементом предиката,
а всего таких элементов 4 - столько же, сколько элементов в области определения.
Последний способ определения предиката будет таким. Выпишем заголовок - имя предиката,
аргументы в скобках, знак равенства и формулу. Все свободные переменные
в формуле должны присутствовать в заголовке среди аргументов ровно по одному разу.
Также там могут быть дополнительные аргументы, которые будем называть избыточными параметрами.
Например:
P(x, y, z) = x & y (2)
Здесь область определения предиката есть декартово произведение областей допустимых значений
для переменных, перечисленных в скобках слева от знака равенства, причем порядок умножения
соответствует порядку перечисления. Каждый кортеж из области определения будет отображаться
предикатом на результат вычисления формулы после подстановки аргументов кортежа на место
соответствующих свободных переменных в формуле справа от знака равенства. Если переменная
избыточная, она просто никуда не подставляется.
Множество значений функции F - это подмножество Y' области значений,
состоящее из таких ее элементов y, для которых существует
x 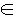 X такой, что F(x) = y.
X такой, что F(x) = y.
Множество истинности предиката F - это подмножество X' области определения,
состоящее из таких ее элементов x, для которых F(x) = true.
В этих двух определениях произвольная функция сведена к формату с одной переменной.
Предикаты классифицируются по множеству значений Y' и множеству
истинности X':
| Тип | Множество значений | Множество истинности | Краткое обозначение |
Тождественно истинный,
общезначимый,
тавтология | Y' = {true} | X' = X | F 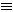 true true |
| Необщезначимый | (Y' = {false})  (Y' = TF) (Y' = TF) | X' ≠ X | F 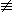 true true |
Тождественно ложный,
невыполнимый
| Y' = {false} | X' = 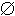 | F 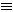 false false |
| Выполнимый | (Y' = {true})  (Y' = TF) (Y' = TF) | X' ≠ 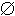 | F 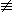 false false |
Нейтральный,
переменный | Y' = TF | (X' ≠ X) & (X' ≠ 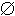 ) ) | F 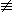 const const |
| Постоянный | (Y' = {false})  (Y' = {true}) (Y' = {true}) | (X' = X)  (X' = (X' = 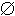 ) ) | F 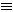 const const |
Предикат удобно обозначать одиночным символом (например, F). Надо особо заметить, что этот символ может быть как переменной,
так и константой. В данном случае предикатной переменной или предикатной константой. Для пояснения проведем аналогию с алгебраическими
функциями. Обозначения sin и cos - это константы. Они обозначают вполне конкретные функции, скажем,
от действительной переменной, которые не могут быть изменены, переопределены, использованы как место для подстановки и так далее.
Теперь возьмем фразу: "Пусть f(x) - некоторая непрерывная функция от действительной переменной..." В этой фразе не только
x, но и f является переменной, обозначающая некоторое заранее неизвестное множество, являющееся непрерывной
функцией. На место f в некоторых случаях может быть подставлена константа sin или cos.
Аналогично обозначения предикатов в виде одиночного символа будут в некоторых случаях константами, а в некоторых - переменными. Если предикат уже полностью
определен через формулу или как множество (через запись в фигурных скобках или другие операции) или через равенство как в
(2), то символ, обозначающий такой предикат, есть предикатная константа. Если предикат не определен полностью,
то символ, обозначающий такой предикат, есть предикатная переменная. Область допустимых значений для такой переменной
- некоторое множество предикатов, заданное каким-нибудь способом.
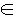 X & y
X & y 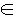 Y
Y Y
Y Y =
Y = 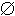
 X2
X2 ...
... Xn
Xn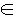 X1 & ... & xn
X1 & ... & xn 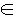 Xn
Xn Y
Y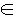 F
F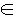 F
F X2
X2 ...
... Xn
Xn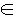 X
X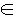 F
F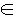 F
F Z
Z Z
Z Z
Z TF
TF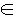 X
X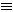 true
true (Y' = TF)
(Y' = TF)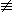 true
true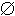
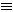 false
false (Y' = TF)
(Y' = TF)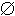
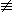 false
false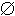 )
)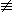 const
const (Y' = {true})
(Y' = {true}) (X' =
(X' =  )
) const
const