Карты Карно
[предыдущая глава]  [оглавление]  [следующая глава]

Упрощение дизъюнктивных форм может показаться кропотливым делом, особенно запоминание многочисленных правил. Для тех, у кого развито пространственное образное мышление, может показаться более удобным использовать так называемые карты Карно, они же диаграммы Вейча. Речь идет о графическом представлении дизъюнктивной формы.

Вид карты Карно зависит от количества переменных в формуле. Существуют карты Карно для 2-6 переменных. Для двух переменных это - просто квадрат 2x2:

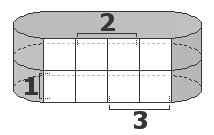
Для трех переменных это - прямоугольник 2x4, склеенный краями в форме цилиндра:

Для четырех переменных надо взять квадрат 4x4, и склеить уже две стороны, получив тор:

Поверхности, закрашенные серым, показывают фигуру, которая должна получиться после склеивания. Для 5 или 6 переменных понадобятся уже не поверхности, а объемные фигуры, например, для 6 переменных - куб со стороной в 4 клетки. Кстати, объемные фигуры можно применять и для меньшего числа переменных: для трех - куб 2x2x2, для четырех - брусок 2x2x4. Мы не будем приводить здесь все эти варианты, так как принцип везде примерно одинаковый.

Нельзя сказать, что карты Карно дают какой-то принципиально новый способ, нет. Геометрические приемы (которые мы ниже рассмотрим), строго соответствуют уже известным нам правилам приведения подобных членов. Однако человеческое мышление устроено так, что с наглядными образами оно работает быстрее и точнее. Рассмотрим принцип работа с картами Карно на примере дизъюнктивных форм с 4 переменными. Рассмотрим квадрат 4x4. Порядок склейки мы рисовать больше не станем, но будем о нем помнить.

Всего в карте Карно должно быть 2N ячеек, где N - число переменных. В данном случае переменных 4 и ячеек 16.

По краям карты пишутся переменные участвующие в формуле или же их номера (1, 2, 3, 4). Условимся, что наша формула содержит переменные x, y, z, t. Для других переменных принцип будет тот же самый. Рядом с переменными нарисованы [-образные фигуры, указывающие область карты, к которой относится переменная. Каждая переменная захватывает ровно половину карты. На следующем рисунке зеленым закрашены области для каждой переменной. Область, закрашенная синим, относится к той же переменной, но с отрицанием:

Константе true соответствует полностью закрашенная карта, а константе false - полностью незакрашенная.

Теперь, когда мы знаем, как закрашивается карта для отдельных переменных и констант, поясним, что происходит с отдельным слагаемым, которое может состоять из нескольких переменных и констант, соединенных операциями "&", то есть, из серии множителей. Для закраски части карты, которая относится к такой серии, надо найти ту часть карты, которая закрашена для каждого из множителей. Вот так, например выглядит множитель x&y&~z. На рисунке каждый из трех множителей показан в виде полупрозрачного "стекла". Над двумя ячейками оказываются все три "стекла", и они окажутся самыми темными. Этот прямоугольник 2x1 как раз и будет соответствовать формуле x&y&~z.

Из этого наглядного приема следуют правила поглощения для множителей. Например x&x - как два одинаковых "стекла", расположенных точно друг над другом. Такая конструкция ничего не изменит: те же самые ячейки окажутся одновременно под всеми стеклами. То есть, x&x = x. Формуле x&~x соответствуют два "стекла", которые не пересекаются между собой. Значит, ни одной ячейки не окажется одновременно под обоими стеклами, получится незакрашенная карта Карно. То есть, x&~x = false. Для формулы x&false можно взять такую аналогию: стекло для "x" и невидимая стеклянная пылинка "false", не способная накрыть даже одну ячейку карты. В результате ни одна ячейка не окажется закрыта обоими стеклами: x&false = false. Формуле true&x соответствует большое стекло, закрывающее всю карту, и стекло, закрывающее часть "x". Оба стекла одновременно будут только над ячейками, покрывающими "x". То есть, x&true = x.

В качестве упражнения попробуйте определить, какие ячейки надо закрасить для трех формул:

  1. ~y
  2. ~y&~x&~z&~t
  3. y&x&z&z&t
  4. x&~t

После того, как определены закрашенные области для каждого слагаемого, остается только "сложить" операциями "". Для этого просто закрашиваются все области, которым соответствует хотя бы одно слагаемое. Например, если объединить в одну дизъюнктивную форму все слагаемые, рассмотренные в предыдущем упражнении:

~y ~y&~x&~z&~t y&x&z&z&t x&~t,    (1)

то получится такая карта:

Перечисленные действия ведут к получению закрашенной карты Карно и представляют собой первый этап упрощения дизъюнктивной формы. Вкратце перечислим шаги, которые надо сделать на этом этапе:

  1. Убрать лишние знаки отрицаний по формуле ~~X = X.
  2. Определить область для каждого множителя.
  3. Для каждого слагаемого, состоящего из нескольких множителей, закрасить область, которая накрывается одновременно всеми этими множителями.
  4. Для всей формулы закрасить область, которая накрывается хотя бы одним из слагаемых.

На втором этапе происходят обратные действия. Надо попытаться представить себе, сколько и каких прямоугольных "стекол" со сторонами 1, 2 или 4 ячейки нужно, чтобы покрыть закрашенную область и только ее. Тут то нам и понадобится хорошее пространственное воображение (особенно, если учесть, что края карты могут быть склеены). После того, как будут определены нужные "стекла", нам останется только выполнить обратные действия и выписать получившуюся формулу. В нашем примере хватит двух "стекол" (учтите, что "стекло" для "~y" склеено по внешней стороне квадрата:

Этим двум стеклам соответствуют слагаемые ~y и x&~t. Следовательно, после упрощения формула (1) примет вид:

~y x&~t.

Вопросы и задания для самостоятельной работы

  1. С помощью карт Карно упростите формулу:
    x&y x&~y t z&x ~t&~t&y
  2. С помощью карт Карно упростите формулу:
    a&b&~c&~c ~c&~a b&a b&c
    Подсказка: в данном случае только три переменных, так что можно обойтись более простой картой 2x4.