Пусть в формуле Ψ есть свободные переменные. Пусть одна из них - γ.
Добавление конструкции
 γ
или
γ
или
 γ
слева от Ψ образует формулу, в которой количество свободных переменных на единицу меньше,
чем в формуле Ψ. Таким образом можно, последовательно связывая одну переменную за другой,
свести число свободных переменных к нулю.
γ
слева от Ψ образует формулу, в которой количество свободных переменных на единицу меньше,
чем в формуле Ψ. Таким образом можно, последовательно связывая одну переменную за другой,
свести число свободных переменных к нулю.
Особенно важен случай, когда при таком последовательном связывании мы используем один и тот же квантор.
В серии одинаковых кванторов их можно менять местами:
 γ
γ  β Ψ =
β Ψ =  β
β  γ Ψ
γ Ψ
 γ
γ  β Ψ =
β Ψ =  β
β  γ Ψ
γ Ψ
Благодаря чему, неважно (для конечного результата вычислений), в каком порядке мы будем связывать переменные. Добавление
слева от формулы серии одинаковых кванторов, которые связывают одну за другой все свободные переменные формулы,
будем называть замыканием формулы. Замыкание будем обозначать кратко квантором без кванторной переменной
(эта запись - сокращение формул РБА, но не сама формула). Пусть в формуле Ψ присутствует n
свободных переменных x1,...,xn. Тогда:
 Ψ =
Ψ =  x1
x1  x2...
x2...
 xn Ψ
xn Ψ
 Ψ =
Ψ =  x1
x1  x2...
x2...
 xn Ψ
xn Ψ
Вычисление таких формул очень просто:
 Ψ = (P
Ψ = (P 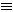 true)
true)
 Ψ = (P
Ψ = (P 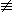 false)
false)
где P - предикат, построенный по формуле Ψ.
Рассмотрим различные свойства замыканий.
Теорема 04.2
Если  (R & S) = true, то (R & S) = true, то  R = true,
и R = true,
и  S = true. S = true.
|
Доказательство
Формула  (R & S), если раскрыть сокращение, содержит некоторое
количество кванторов слева: 0 штук или более. Среди них будут кванторы с кванторными переменными трех видов: (R & S), если раскрыть сокращение, содержит некоторое
количество кванторов слева: 0 штук или более. Среди них будут кванторы с кванторными переменными трех видов:
- которые есть в формуле R среди свободных переменных (но не в S) - пусть это для определенности
переменные r1,...rn.
- которые есть в формуле S среди свободных переменных (но не в R) - пусть это для определенности
переменные s1,...sm.
- которые есть в обоих формулах и S, и R среди свободных переменных - пусть это для определенности
переменные t1,...tl.
Если  (R & S) = true, это означает, что существует комбинация значений для переменных
r1,...rn, s1,...sm, t1,...tl, при которой
(R & S) = true.
Пусть одна из этих комбинаций: r'1,...r'n, s'1,...s'm, t'1,...t'l. (R & S) = true, это означает, что существует комбинация значений для переменных
r1,...rn, s1,...sm, t1,...tl, при которой
(R & S) = true.
Пусть одна из этих комбинаций: r'1,...r'n, s'1,...s'm, t'1,...t'l.
Согласно таблице истинности для операции "&", (R & S) = true только в том случае,
когда R = true и S = true.
При этом в R подставляются значения для переменных
r'1,...r'n, t'1,...t'l.
Следовательно, по крайней мере при подстановке такой комбинации значений R = true. Отсюда следует,
что  R = true. R = true.
Аналогично, в S подставляются значения для переменных
s'1,...s'm, t'1,...t'l.
Следовательно, по крайней мере при подстановке такой комбинации значений S = true. Отсюда следует,
что  S = true. S = true.
|
Обратная теорема неверна. Так, если область допустимых значений для переменных x и y есть TF,
то  x = true и
x = true и  ~x = true, но
~x = true, но
 (x & ~x) = false.
(x & ~x) = false.
Теорема 04.3
 (R & S) (R & S)  ( ( R & R &  S) S)
|
Доказательство
Как и в прошлый раз выделим свободные переменные:
- которые есть в формуле R (но не в S) - пусть это для определенности
переменные r1,...rn.
- которые есть в формуле S (но не в R) - пусть это для определенности
переменные s1,...sm.
- которые есть в обоих формулах и S, и R - пусть это для определенности
переменные t1,...tl.
Сначала докажем равносильность в одну сторону, т.е., докажем, что если истинна левая часть, то истинна и правая.
Пусть левая часть истинна. Возьмем произвольную комбинацию значений свободных переменных, входящих в R.
Обозначим их как r'1,...r'n, t'1,...t'l.
Тогда после подстановки этих значений в формулу R и вычисления формулы, должно получаться true. Если бы это было не так
(от противного), то после подстановки комбинации
r'1,...r'n, s'1,...s'm, t'1,...t'l
(где s'1,...s'm - произвольные значения, допустимые для переменных
s1,...sm) в формулу (R & S) и вычисления формулы, получалось бы
false & S = false. А этого не может быть по условию. Итак, для произвольно взятой комбинации значений
свободных переменных, входящих в R, эта формула получается равной true. Следовательно  R = true. R = true.
Аналогично доказывается, что  S = true. S = true.
Теперь докажем равносильность в обратную сторону. Пусть истинна правая часть условия.
Возьмем произвольную комбинацию значений свободных переменных, входящих в (R & S).
Обозначим их как r'1,...r'n, s'1,...s'm, t'1,...t'l.
При вычислении R & S сначала вычислим R. В нее будет подставлена комбинация значений
r'1,...r'n, t'1,...t'l.
Должно получиться true, а иначе (от противного)  R = false и тогда R = false и тогда
 R & R &  S = false & S = false &  S = false.
Аналогично доказываем, что вычисление S дает true. Тогда (R & S) = (true & true) = true.
Итак, для произвольно взятой комбинации значений свободных переменных, входящих в (R & S), эта формула получается
равной true. Следовательно S = false.
Аналогично доказываем, что вычисление S дает true. Тогда (R & S) = (true & true) = true.
Итак, для произвольно взятой комбинации значений свободных переменных, входящих в (R & S), эта формула получается
равной true. Следовательно  (R & S) = true. (R & S) = true.
|
Теорема 04.4
Если  R = true и R = true и  (R (R  S) = true,
то S) = true,
то  S = true S = true
|
Доказательство
Как и в прошлый раз выделим свободные переменные:
- которые есть в формуле R (но не в S) - пусть это для определенности
переменные r1,...rn.
- которые есть в формуле S (но не в R) - пусть это для определенности
переменные s1,...sm.
- которые есть в обоих формулах и S, и R - пусть это для определенности
переменные t1,...tl.
Возьмем произвольную комбинацию свободных переменных, входящих в S. Обозначим ее
s'1,...s'm, t'1,...t'l.
Подставим ее в S и допустим (от противного), что получится false.
Возьмем теперь произвольную комбинацию допустмых значений для переменных r1,...rn,
и обозначим эти значения r'1,...r'n.
Составим комбинацию
r'1,...r'n, s'1,...s'm, t'1,...t'l
Подставим ее в формулу R  S. При этом в R будут подставлены
r'1,...r'n, t'1,...t'l и должно
получиться true, так как в условии S. При этом в R будут подставлены
r'1,...r'n, t'1,...t'l и должно
получиться true, так как в условии  R = true, а значит, подстановка любых
комбинаций значений переменных в R должна давать результат true.
При этом в S будут подставлены s'1,...s'm, t'1,...t'l и,
согласно сделанному допущению, должно получиться false. В результате R R = true, а значит, подстановка любых
комбинаций значений переменных в R должна давать результат true.
При этом в S будут подставлены s'1,...s'm, t'1,...t'l и,
согласно сделанному допущению, должно получиться false. В результате R  S = true S = true  S = false.
Получается, что подстановка комбинации r'1,...r'n, s'1,...s'm, t'1,...t'l
в формулу R S = false.
Получается, что подстановка комбинации r'1,...r'n, s'1,...s'm, t'1,...t'l
в формулу R  S дает fals, а значит, формула S дает fals, а значит, формула  (R (R  false) = false.
Это противоречит условию, значит, наше допущение неверно и S = true. При этом мы рассматривали произвольную
комбинацию значений переменных. Значит, S = true для любой комбинации, значит, false) = false.
Это противоречит условию, значит, наше допущение неверно и S = true. При этом мы рассматривали произвольную
комбинацию значений переменных. Значит, S = true для любой комбинации, значит,  S = true. S = true.
|
Заметим, что формулировка последней теоремы представляет собой разновидность modus ponens.
 γ
γ γ
γ γ
γ  β Ψ =
β Ψ =  β
β  γ Ψ
γ Ψ γ
γ  β Ψ =
β Ψ =  β
β  γ Ψ
γ Ψ Ψ =
Ψ =  x1
x1  x2...
x2...
 xn Ψ
xn Ψ Ψ =
Ψ =  x1
x1  x2...
x2...
 xn Ψ
xn Ψ Ψ = (P
Ψ = (P 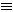 true)
true) Ψ = (P
Ψ = (P 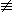 false)
false) x = true
x = true ~x = true
~x = true (x & ~x) = false
(x & ~x) = false (
( S) = true
S) = true